多边形扩展算法实现

最近在实现一个工程绘图功能，给定参数绘制出场景后，用户可对场景设置一定尺寸的宽度，设置宽度后，场景每个坐标顶点会发生变化。

// 由四个顶点构成的多边形
const pointList = [[0, 0], [0, 10], [10, 10], [10, 0]]
// 以上多边形，边缘扩大1后，计算新的顶点坐标集合
const expandWidth = 1

算法原理

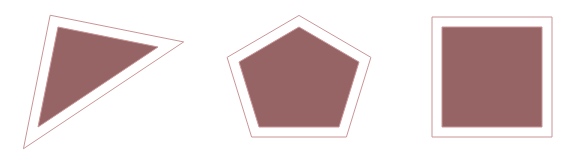
要扩展凸多边形，请绘制一条与每条边平行且距离给定单位数的线。然后使用新线的交点作为展开多边形的顶点。最后的 javascript/canvas 遵循此功能分解：

以下我们定点的结构为：

type IPoint = [number, number]
type IPolyonPoints = IPoint[]

寻找定点

找出哪一边是“出局”，顶点（点）的顺序很重要。在凸多边形中，它们可以按顺时针 (CW) 或逆时针 (CCW) 顺序列出。在 CW 多边形中，将其中一条边逆时针旋转 90 度以获得朝外的法线。在逆时针多边形上，改为顺时针旋转。

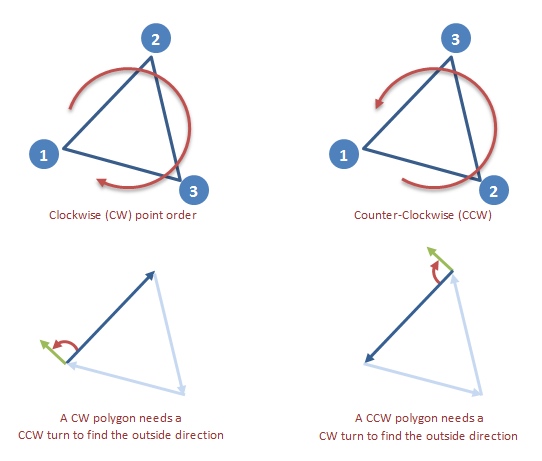
如果顶点的转弯方向事先未知，请检查第二条边如何从第一条边转弯。在凸多边形中，其余边将继续沿相同方向转动：

找到第一条边的 CW 法线。我们还不知道它是朝内还是朝外。

计算第二条边与我们计算的法线的点积。如果第二条边变成 CW，则点积将为正。否则为负。

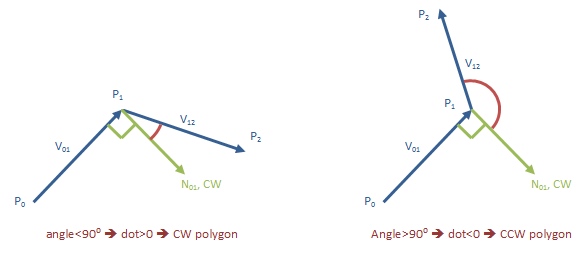
算法表达

function vecDot(v1: IPoint, v2: IPoint) {
  return v1[0] * v2[0] + v1[1] * v2[1];
}

function vecRot90CW(v: IPoint): IPoint {
  return [v[1], -v[0]]
}

function vecRot90CCW(v: IPoint): IPoint {
  return [-v[1], v[0]]
}


function polyIsCw(p: IPoint[]) {
  return vecDot( vecRot90CW( [ p[1][0] - p[0][0], p[1][1] - p[0][1] ]), [ p[2][0] - p[1][0], p[2][1] - p[1][1] ]) >= 0;
}

var rot = polyIsCw(p) ? vecRot90CCW : vecRot90CW;

找到平行于多边形边的线

现在我们知道哪一边在外面，我们可以计算与每个多边形边平行的线，正好是所需的距离。这是我们的策略：

对于每条边，计算其朝外的法线

标准化法线，使其长度成为一个单位

将法线乘以我们希望扩展多边形与原始多边形的距离

将相乘法线添加到边缘的两端。这将为我们提供平行线上的两个点。这两个点足以定义平行线。

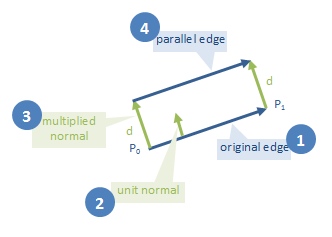
function vecUnit(v: IPoint): IPoint {
  var len = Math.sqrt(v[0] * v[0] + v[1] * v[1]);
  return [v[0] / len, v[1] / len]
}

function vecMul(v: IPoint, s: number): IPoint {
  return [ v[0] * s, v[1] * s ]
}

var v01 = [ pt1[0] - pt0[0], pt1[1] - pt0[1] ];  // edge vector
var d01 = vecMul(vecUnit(rot(v01)), distance);     // multiplied unit normal
var ptx0 = [ pt0[0] + d01[0], pt0[1] + d01[1] ]; // two points on the
var ptx1 = [ pt1[0] + d01[0], pt1[1] + d01[1] ];

计算平行线的交点

–这些将是扩展多边形的顶点。

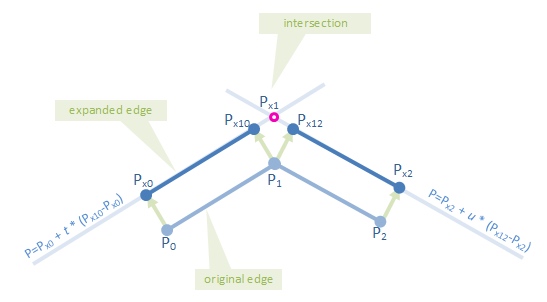
数学：

通过两点P1、P2 的直线可以表示为：

P = P1 + t * (P2 - P1)

两条线可以描述为

P = P1 + t * (P2 - P1)
P = P3 + u * (P4 - P3)

它们的交点必须在两条线上：

P = P1 + t * (P2 - P1) = P3 + u * (P4 - P3)

这可以被按摩成这样：

(P2 - P1) * t + (P3 - P4) * u = P3 - P1

其中在 x,y 方面是：

(P2.x - P1.x) * t + (P3.x - P4.x) * u = P3.x - P1.x
(P2.y - P1.y) * t + (P3.y - P4.y) * u = P3.y - P1.y

由于点 P1、P2、P3 和 P4 是已知的，因此以下值也是已知的：

a1 = P2.x - P1.x    a2 = P2.y - P1.y
b1 = P3.x - P4.x    b2 = P3.y - P4.y
c1 = P3.x - P1.x    c2 = P3.y - P1.y

这将我们的方程缩短为：

a1*t + b1*u = c1
a2*t + b2*u = c2    

求解t得到我们：

t = (b1*c2 - b2*c1)/(a2*b1 - a1*b2)

这让我们可以在处找到交点P = P1 + t * (P2 - P1)。

代码：

function intersect(line1: IPoint[], line2: IPoint[]) {
  var a1 = line1[1][0] - line1[0][0];
  var b1 = line2[0][0] - line2[1][0];
  var c1 = line2[0][0] - line1[0][0];

  var a2 = line1[1][1] - line1[0][1];
  var b2 = line2[0][1] - line2[1][1];
  var c2 = line2[0][1] - line1[0][1];

  var t = (b1 * c2 - b2 * c1) / (a2 * b1 - a1 * b2);

  return {
    x: line1[0][0] + t * (line1[1][0] - line1[0][0]),
    y: line1[0][1] + t * (line1[1][1] - line1[0][1])
  };
}

处理特殊情况

有许多特殊情况值得关注。如当两条边之间的角度非常锐利时，扩展的顶点可能与原始顶点相距很远。如果超出某个阈值，您可能需要考虑裁剪扩展边缘。在极端情况下，角度为零，这表明扩展顶点在无穷大处，导致在算术中被零除。小心。

当前两条边在同一条线上时，您无法通过查看它们来判断它是 CW 还是 CCW 多边形。查看更多边缘。